一、故事的开端
2024-03-07
我们的探索大概可以从 2013 年开始讲起。当时,自然语言处理里有一种词嵌入技术被发展出来,引发了大量的研究与讨论。 它最吸引人的地方在于这种分布式表征的词向量,可以捕捉到词语之间的语义关系,被称为“正则性”(regularity)。 正则性是指,如果两对词语在语义关系上有相似性,那么它们的词向量之间的关系也有几何上的平行性。 正则性是词语关系的一种几何化表达,它是词向量的一个重要性质。
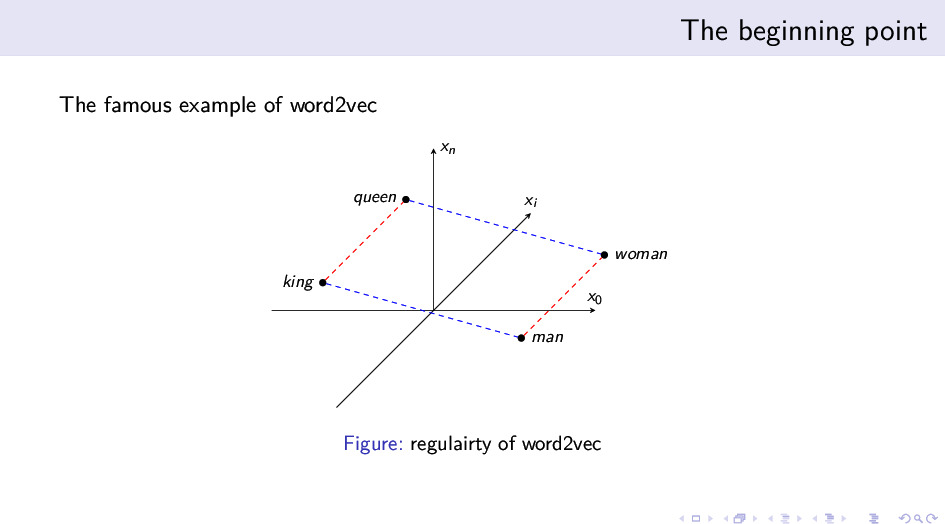
最为著名的例子是“男人”和“女人”之间的关系,与“国王”和“王后”之间的关系。这两对词语之间的关系是相似的,所以它们的词向量之间的关系也应该是平行的。 在上图的例子中,我们可以看到两组平行关系:
- 性别维度移动:男人 - 女人 ≈ 国王 - 女王
- 王权维度移动:国王 - 男人 ≈ 女王 - 女人
这两组关系之间的平行性,形成一个平行四边形。同时,这两组平行关系也可以看成一种关系矢量上的运算,用几何语言说就是:
- 男人 + 性别维度移动 + 王权维度移动 = 女王
- 男人 + 王权维度移动 + 性别维度移动 = 女王
也就是说:
- 性别维度移动 + 王权维度移动 = 王权维度移动 + 性别维度移动
这反映了关系运算的交换律。
当时的算法对这种关系正则性的捕捉是有限的,以后的技术发展也没有沿着这个方向继续前进,而是转向了更加复杂的模型和任务。我思考的起点就恰恰是从这里延伸出来的。 如果我们把这种关系正则性强制要求下来,会发生什么呢?
2015 年的秋天,我去拿数字和数字的运算关系做了一些尝试,但很快就发现它存在一些困难。

这个困难可以表述为两点:运算关系不具备交换性,从而无法形成平行四边形;欧式空间的容量是有限的,无法容纳指数爆炸的运算关系组合。 让我们举例子来说明一下,我们考察简单的“+1”和“x2”的关系。此时,所有的数字都映射为空间的点,而“+1”和“x2”运算关系映射为空间的向量。
从一个点 $\alpha$ 出发,我们可以进行一系列的运算关系组合,比如:
- 先“+1”再“x2”操作:$(\alpha +1) \times 2 = 2 \alpha + 2$
- 先“x2”再“+1”操作:$\alpha \times 2 + 1 = 2 \alpha + 1$
不论我们从哪个点出发,这两个运算关系都不具备交换性,所以它们无法形成平行四边形。 平行四边形的存在也意味着两次关系运算的组合中可以约化掉一个,从而可以避免运算关系组合的指数爆炸。 而关系不具备交换性,平行四边形就无法形成,指数爆炸的运算关系组合也就无法避免。
如果每个特征在表征空间里都占据有限大的体积,且这个有限大的体积存在一个最小的分辨限制,那么组合爆炸就意味着我们需指数增长的体积来容纳这些运算关系的组合。 在欧式空间里,球体的体积随着半径增长是多项式级别增长的,所以随着表达式数量的增加,表征空间会很快不足够使用。
幸运的是,几何学里有一种空间,它的容量是指数增长的,同时它里面也不存在平行四边形构造,这就是双曲空间。我决定拿双曲空间来尝试解决这个问题。
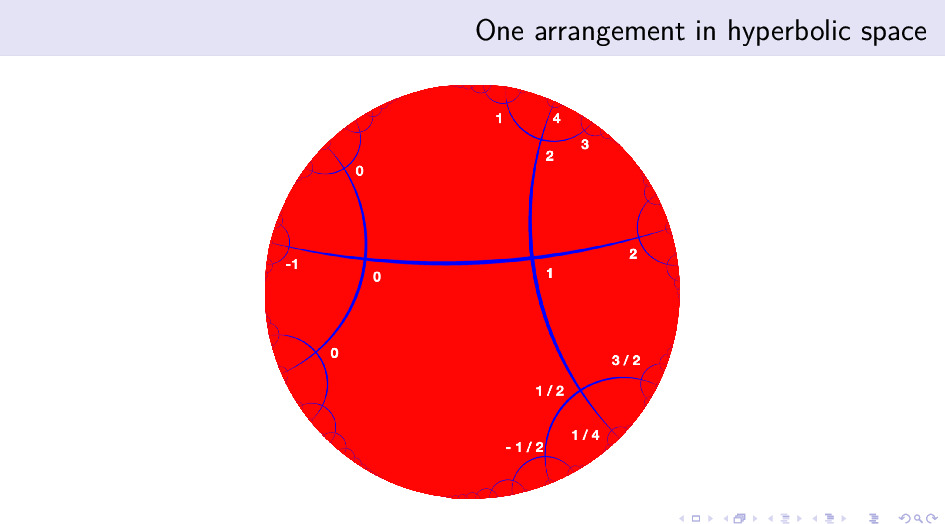
经过一些尝试,我很快就发现,一种称之为四阶无限边形铺嵌的结构可以用来编码一些数字的加法和乘法。如上图,横着的最主要的那根轴是加法轴,数字按照加法的规律从左到右不断加一排布; 与之垂直的轴是乘法轴,数据按照乘法的规律逐步乘二排布。与乘法轴垂直的都是加法轴,而与加法轴垂直的都是乘法轴。通过这种加乘交错的构造我们可以编码数字的加法和乘法运算。
当这个数字的四阶无限边形排布做出来以后,望着这些高度对称分布的点值,我产生了非常自然的一个疑问和推测,这些离散点值能否连续扩展到整个庞加莱圆盘? 如果这些点值能连续的分布在整个庞加莱圆盘上,那么我们就可以用它来编码所有实数值的算术运算了。 此后,我就一直在业余时间对相关的问题进行探索,陆陆续续有了一些收获。但这个最初的问题,我至今还没有完全解决。 有朋友告诉我,它可能和一些复杂的模函数有关系。
时间飞逝到了 2019 年,我在出差的飞机上,突然想到既然我希望这些点值能够连续的分布在整个庞加莱圆盘上,那么为什么我不试一下无穷小的生成过程呢? 我在飞机上快速做了一些推导,结果是正面的。旅途结束后的几天,我就得到了一个微分方程,它描述了一个加法和乘法的双生成元的无穷小生成过程。

整个推导非常初等,只是极限过程和微元的基本运算。因为这个方程刻画了一个计算的流动过程,所以我称之为“流方程”。

流方程是可解的,解刻画了一个连续生成过程,再稍微分析一下就可以发现这个连续生成过程里容纳一个离散生成过程,刚好对应前面双曲圆盘里的四阶无限边形结构。 这一点我们会在后面的章节里详细讨论。
2021 年春天,我得到公司(彩云科技)的支持,和两个实习生一起工作了三个月,做了一些更加严谨的研究。来自山东大学的张乐同学利用分离变量法很快推导出了一个流方程的解析解。
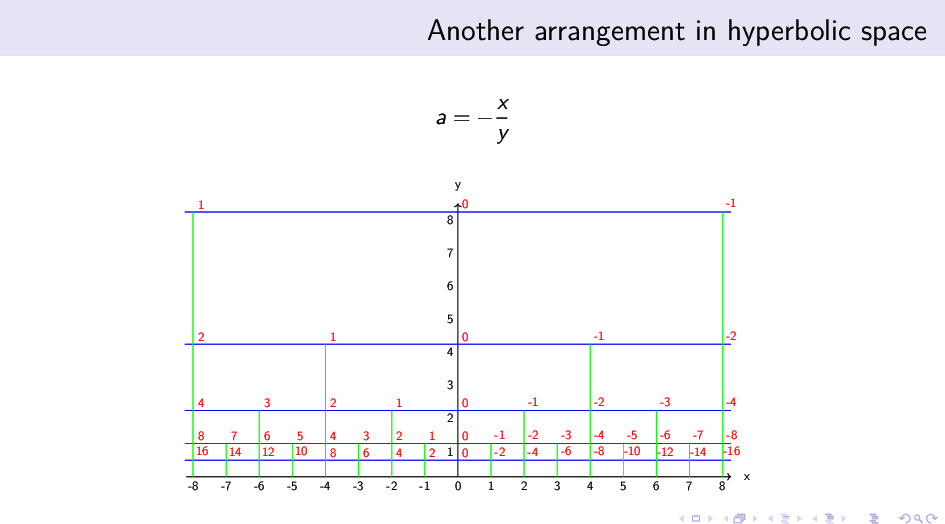
在这个解析解之前,我们仅有一些猜测,比如庞加莱圆盘里的四阶无限边形结构,它只是知道离散结构,但不知道连续结构。 而张乐给出的解析解,让我们第一次有了一个可以仔细研究的严格数学对象。我经过一些尝试,画出了这个解析解的图像,发现它的离散生成关系, 和一种称为 Baumslag–Solitar 群的生成关系是一致的,于是也就有了上图。
在上图中,我们首先可以看到一些红色的离散点值$a$,它们符合解析式 $a = -\frac{x}{y}$。 蓝横线是伪圆,它们从右向左按照加一的规律不断增长,代表了一条条的加法轴。 绿竖线是测地线,它们从上向下按照乘二的规律不断增长,代表了一条条的乘法轴。 蓝横线和绿竖线交错排布,彼此垂直。
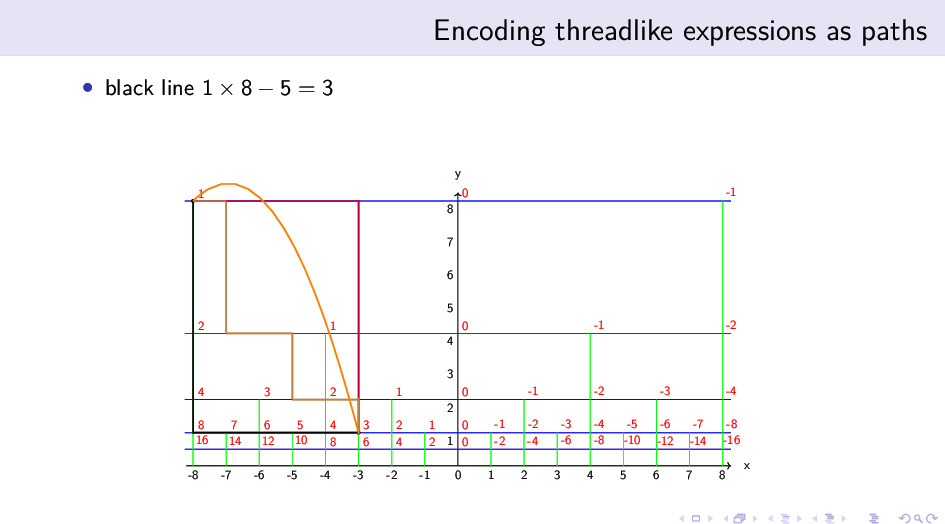
因为蓝横线和绿竖线交错的网格的存在,我们可以利用它来编码一些数值的算术运算。比如 $1 \times 8 - 5 = 3$,我们可以在网格上画出这个算术运算的路径。 从任何一个 $a$ 值为 $1$ 的点出发,向下走三步,完成三次乘二操作,然后向右走五步,完成减五的操作,就会到达一个 $a$ 值为 $3$ 的点,也就是上图中黑色的线。
完全类似的,上图中紫红色的线编码了 $(1 - \frac{5}{8}) \times 8 = 3$ 的算术运算; 褐色的线编码了 $(((1 - \frac{1}{8}) \times 2 - \frac{2}{4}) \times 2 - 1) \times 2 = 3$ 的算术运算。
上面的例子都是折线,那么有趣的问题是橙色的曲线编码了什么?仔细考虑一下,就会意识到它编码了一种特别的、不同于传统的黎曼积分的积分过程。黎曼积分只是累加小量; 而这个曲线代表的积分过程会同时累加小量和累乘小量,加法的小量是指趋近于零的量,而乘法的小量是指趋近于一的量。
