一角

二、基本概念与示例

本节我们作更加严格的讨论，引入一些基本概念，然后展示一些示例性的算术表达式空间。

算术表达式

从计算机科学的角度来看，算术表达式是一种抽象的递归数据类型，它可以被解析成为一棵树。这棵树的叶子节点是操作数，内部节点是操作符。 所以也可以说，算术表达式有字串表示和树表示两种形式，常见的形式是字串表示，基于中缀表示法和括号的优先级规则。

我们尝试在有理数域 $Q$ 上给出算术表达式的定义。这是一种生成式的递归定义方式，它说明：

• 有理数本身就构成算术表达式
• 算术表达式的加、减、乘、除组合仍然构成算术表达式

纯数学专业的读者可能会不熟悉这种定义方式，可以参考形式语言里的生成式定义，我们这里终止符号是有理数、括号和四则运算符号。

在这个递归生成结构上也可以递归定义一个求值的过程，可以理解成表达式树表示上的一种遍历过程。一般来讲，这个遍历的求值过程不唯一。 但是同一个表达式树的求值结果是唯一的。

然而有一些算术表达式的求值过程是唯一的，比如下图展示的向左或者向右展开的可线索化表达式。 可线索化表达式是指一类算术表达式，它的左支或者右支全部都是叶节点。这种表达式的求值过程是唯一的。向左或者向右展开完全是对称的， 向左展开的形式在求值时是从头计算到尾，向右展开的形式在求值时是从尾计算到头。这里我们取向左展开作为标准形式。

细心的读者可能已经注意到，我们的算术表达式时是定义在有理数域上的，为什么不能直接定义在实数域呢。原因是我们在定义表达式的除法时，必须要求除数不为零。 而在有理数域上，一个子表达式是否为零是可以判定的。在实数域上，表达式是否为零不可判定的。为了使概念的定义完整，我们先把算术表达式定义在有理数域上。 然后再通过适当的完备化的手法，把它推广到实数域上。这里有理数域的选择，其实反映了语法与语义的差别。我们算术表达式的递归定义是纯粹的语法式的， 为了回避语义上的困难，我们不得不选择有理数域。

下面我们讨论算术表达式的离散生成关系如何做成群的。我们引入离散的加法和乘法生成元，在自由生成下，可以得到一个表达式上的群结构（注意是表达式上的，不是值上的群结构）。 这个过程在几何上得到一些由特定正交线族上的折线构成的路径，这为后继的讨论提供了第一步的基础。

下面考察这个自由群的交换子，交换子刻画了群的不可交换性。这里我们考察生成元构成的交换子，如下有几种不同的引进方式。 我们把第三种方式称为“算术扭曲”，因为直观上，这种加法和乘法上的不可交换性，造成了几何空间的扭曲。 需要指出，因为生成元带来的运算被解释为几何上的路径，那么算术扭曲也是一种定义在几何路径上的量。

流方程

和前一节讨论的有理数域上的表达式不同，在那里我们做了准备和铺垫，希望通过完备化来构造出算术表达式的几何空间。这是一种构造性的途径和研究方法。 本节则有所不同，我们在这里使用微积分的工具，直接在几何空间上讨论一个标量场$a$，称为赋值场，这个场满足流方程，可以证明前一小节讨论的离散路径群结构可以嵌入到这个几何图景里。 这两种不同的途径都是我们研究的工具。

我们在最初引入流方程的时候，使用的是局部极坐标系；类似，我们也可以引入对应的局部笛卡尔坐标系；甚至，我们也可以推导出梯度线-等值线坐标系。 在这些坐标系里，流方程有不同的形式，但是它们都是等价的。这是因为流方程是赋值场 $a$ 的局部性质，它本身不依赖于坐标系的选择。

这些局部的坐标系可以刻画赋值场 $a$，同样也可以通过第一基本形式来刻画几何空间本身。我们需要指出， 这些局部刻画需要一个全局的适配条件才能拼接成一个整体的刻画。

形式上，流方程是可以解出来的，不同坐标系下的解会带给我们不同的几何图景。

局部极坐标系下的解，我们通过泰勒展开、变形、引入倍角公式的处理，最终得到了一个公式。 仔细观察这个公式会发现，它在 $\theta$ 角取值为 $0$、$\frac{\pi}{2}$、$\pi$、$\frac{3\pi}{2}$ 时，分别编码了加减乘除四种运算。 如此，我们就可以把算术表达式离散生成的群结构作为路径嵌入到这个几何空间里。

局部梯度线-等值线坐标系下的流方程也是可解的。对于以 $0$ 值为起点的情形，我们发现此时的解和双曲空间中圆的周长公式形式是一样的，只差一个比例系数。 这给我们带来了一种扩散圆的几何图景，扩散圆的周长乘以某个比值就是赋值场。 直观上，当有多个零点或者零点构成零线时，我们使用惠更斯原理，用这些扩散圆的叠加，也就是波前来刻画赋值场。 目前这个几何图景还只是一种观察，尚未得到严格的证明。

第一类算术表达式空间

张乐通过分离变量法得到了第一类算术表达式空间的解析解。我们对这个解析解进行了分析。在上半平面模型里， 不论加法生成元 $\mu$ 还是乘法生成元 $e^\lambda$ 的取值怎么变化，我们只需要变化空间的度规，赋值场 $a$ 始终是同一个解析解 $-\frac{x}{y}$。 此时，流方程是成立的。

我们把如上情况下的几个数学对象综合到一起考虑作为一种更高层的数学对象：

• 实数域 $\mathbb{R}$
• 其上的可线索化表达式 $E[\mathbb{R}]$
• 所在的指定了度规的双曲空间$H$
• 标量的赋值场 $a$
• 所有的路径集合 $P$
• 路径集合可以解释为积分的集合 $I$

于是结构 $(\mathbb{R}, E[\mathbb{R}])$ 代表了这个数学对象的算术表达式的侧面；$(H, P)$ 代表了这个数学对象的几何侧面； $(a, I)$ 代表了这个数学对象的分析学和函数论的侧面。

我们把这个综合的数学对象称为算术表达式空间。而如上设定的算术表达式空间是第一类的实例，称为第一类算术表达式空间。

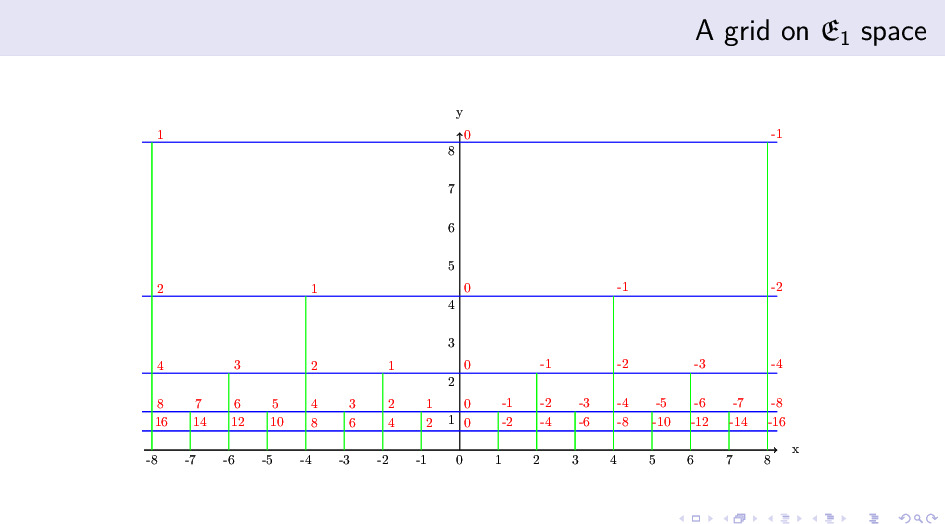
我们可以在双曲空间 $H$ 画出来由加法生成元和乘法生成元生成的离散的群的 Cayley 图。这个图能清晰的揭示局部结构怎么黏贴整合成一个整体的结构。 因为我们得到的离散的群是 Baumslag–Solitar 群，上图的模式在之前的研究中出现过。问题是，我们能把这个黏贴整合的过程写出来吗？怎么从四阶 Cayley 树粘合出上图？

另一个有趣的问题是，针对同一个算术表达式空间，上图是唯一的吗？ 答案是否定的。

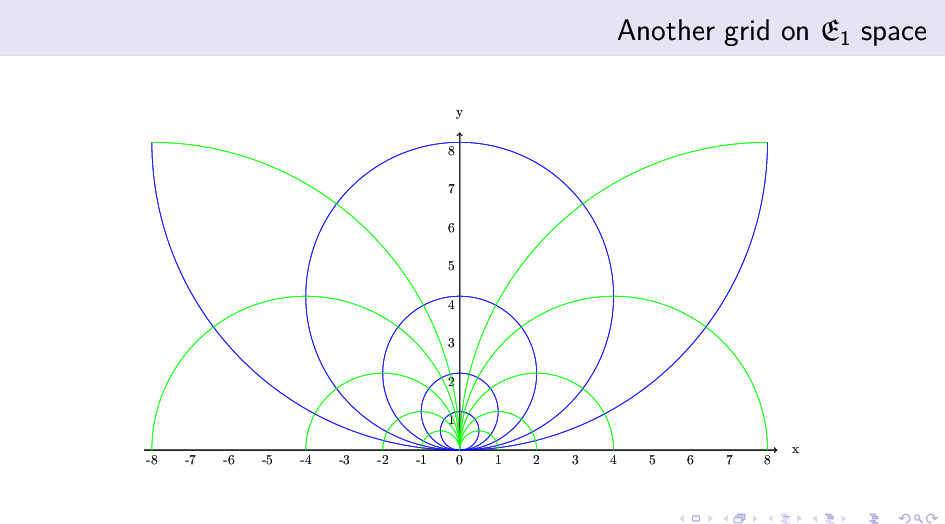
我们还能找到另外一个 Cayley 图。这两个 Cayley 图不但作为图是同构的，而且还共享同一组梯度线-等值线坐标网。

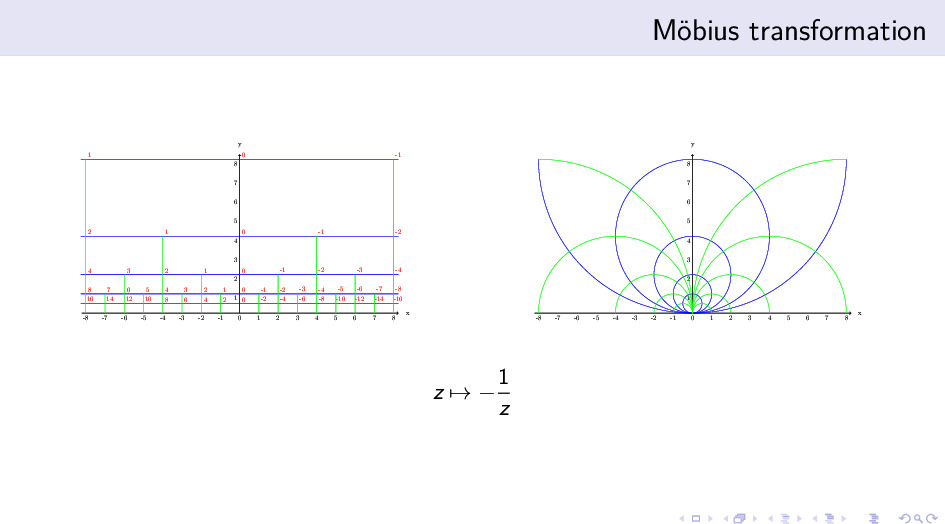
更有趣的是，它们能被一个共形变换联系起来。这不禁让我们思考：

• 为什么是这样两组 Cayley 图？它们有什么联系？背后有什么原因吗？
• 除了 Möbius 变换的写法，我们能用算术表达式的表征来写共形变换吗？比如，用某种算术表达式的变形，可以把这个共形变换写出来？

为了展示这个领域在分析学和函数论方面的丰富性，我们指出赋值场 $a$ 是 Laplacian 的特征函数。但这是个普遍结论还是只在第一类算术表达式空间成立呢？ 目前我们还不清楚。