一角

三、进一步研究—几何篇

在思考的过程中，我们逐步有了一种想法：算术和几何是彼此适配的，在一定程度上，它们可以相互表达。我们需要找到一块落脚的石头去探索这种想法。 经过考虑，我想去试一下，从算术的角度，去定义、刻画、计算几何上的曲率。

在 第 1 节 我们讨论交换律如何约化掉一些关系的组合时，其实我们已经用了算术扭曲的概念， 只是在 第 2 节 我们才正式把这个概念引入。在平面的时候可交换，算术扭曲为零；在双曲的时候，算术扭曲非零。 一个很自然的想法，算术扭曲会不会和曲率有关呢？

很容易理解算术扭曲是定义在路径上的一种量，但是一个偶然的机会，我们发现，在第一类算术表达式空间中，如果我们以一定的倍数放大生成元的步数，我们能把这个边上的量和面积联系起来。

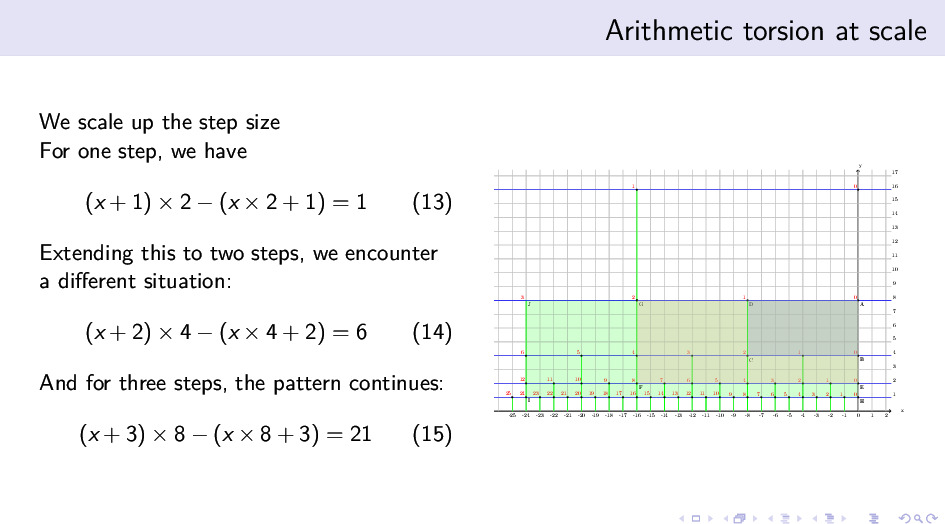
一步、两步和三步情况下的算术扭曲分别是 1、6、21，我们发现这些数也刚好是一步、两步和三步情况下步长所囊括的区域的面积。 这是一个非常让人兴奋的迹象，因为 Gauss-Bonnet 定理也是把两种曲率和区域的面积与边缘彼此联系起来的。我们能不能做类似的事情？

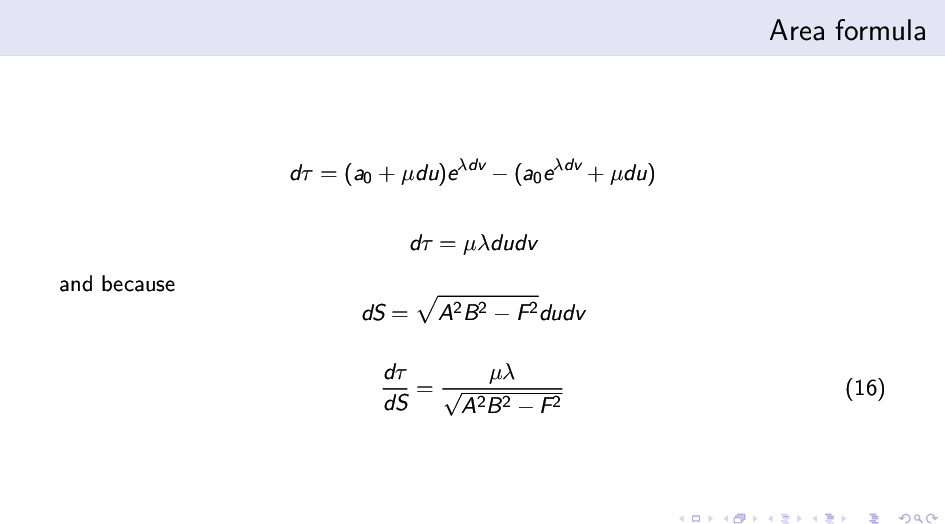
我们进一步分析无穷小版本的算术扭曲，发现它是一个二阶小量，确实和面积有一定的关系。我们能不能积分小量得到？ 但是边上的量的积分需要通过几何上的圈来实现，才能和面积的边缘彼此对应。算术扭曲定义在边上，但它不构成圈。 我们需要找到一种圈上的二阶小量。

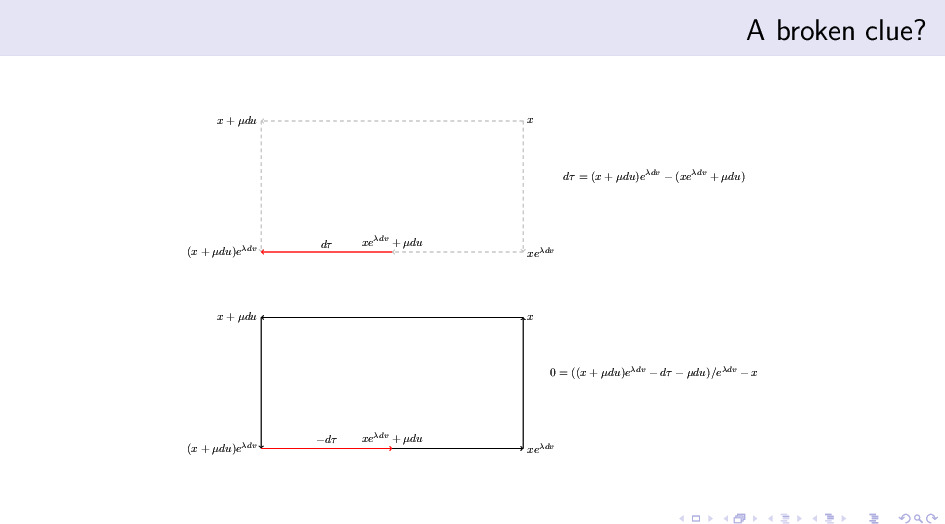
让我们先试验一下，能不能画出来一个有意义的圈。